
This might may not be the most technical but it's the easiest way to remember it! The easiest way to calculate the formal charge of an atom is to do (# of valence electrons - # of dots - # of dashes).
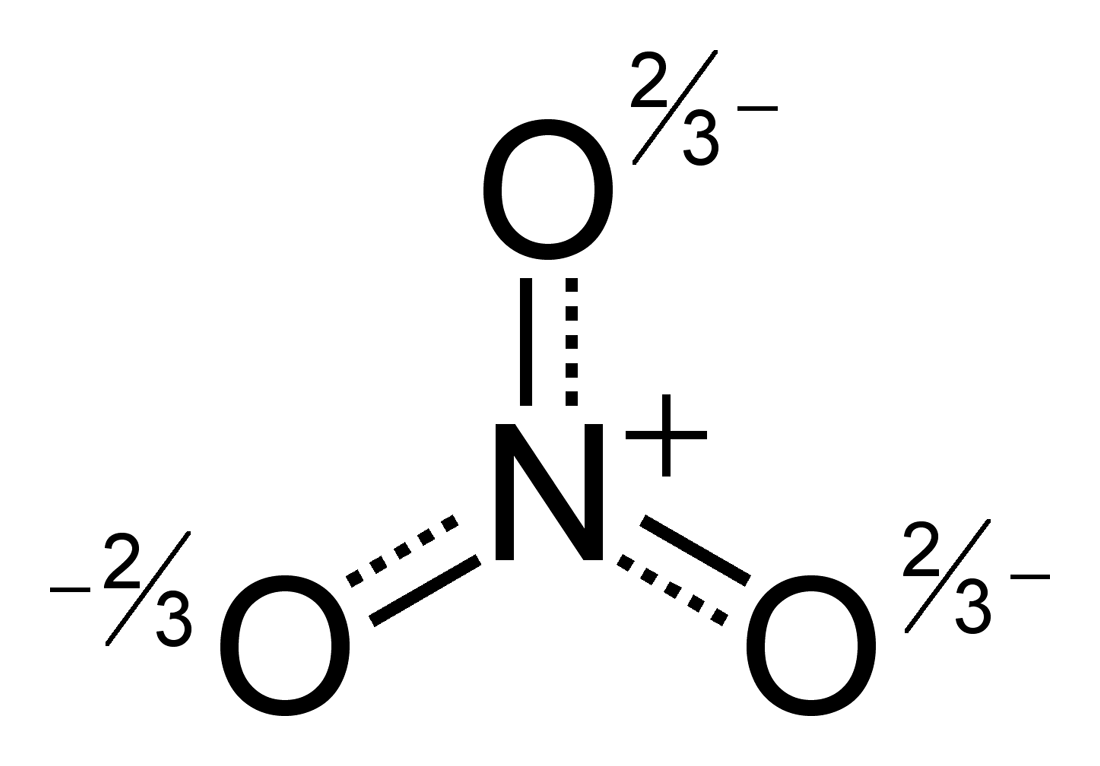
The -1 charge indicates that there is one more electron, so there must be a total of 24 valence electrons represented in the LDS.ĭraw the central atom, which in this case, is nitrogen since there is only one nitrogen atom.ĭraw the 3 oxygen atoms surrounding nitrogen and three single bonds connecting them to nitrogen. But.NO3- is a polyatomic ion and there is a charge attached to the molecule as a whole. Since there are three oxygen atoms, we must account for each: 5+6+6+6 = 23. Recall some steps for this process that we discussed in the last study guide:Ĭount the number of valence electrons that the molecule has in total. Let's try drawing the lewis dot structure (LDS) of the polyatomic ion NO3.

How do you know when a structure has resonance? This will make more sense as we take a look at several examples. However, resonance is all about representing a molecule in varying ways just to make it clear that the molecule is actually an average of those representations in space. It can be applied not only to benzene, but also to other compounds such as ozone and carbocations.A common misconception is that structures that have resonance are truly able to exist with different bond connections. Resonance plays an important structural role in covalent compounds in accordance with valence bond theory. The reason for the intermediate bond length in benzene is due to the fact that these bonds are effectively intermediate in identity between single and double bonds. This actually strengthens the structure, because what appear to be simple #"C - C"# single bonds actually experience double bonded properties instantaneously. Because of this, valence bond theory postulates that the structure resonates: it holds in one formation for an instant, before moving onto the next one, then back again, because neither one is more stable than the other. When this happens in benzene, we see an alternating pattern of #"C - C"# single bonds and #"C = C"# double bonds, as shown in the first diagram.īut a p atomic orbital on, say, #"C"^1#, can overlap with, to form a #pi# bond, a p orbital on #"C"^2# or #"C"^6#, can it not? Upon consideration, neither of the two local carbon atoms is any more favorable than the other for this purpose. In doing this, the overlapping regions will result in a single #pi# bond that contains a pair of bonding electrons. Recall that #pi# bonds result from the extension of half-filled, unhybridised p atomic orbitals from the bonding plane, which can overlap side-on - perpendicular to the #sigma# bond. How can this be? Molecular orbital theory is able to explain this, because resonance is integral to its conception, but valence bond theory must take a different tact if it wishes to explain this. Not only that, but all of the bonds have the same bond length. Yet the bond length shown in benzene is #139"pm"#. The bond length of a #"C - C"# single bond is #154"pm"#, whilst the bond length of a #"C = C"# double bond is #133"pm"#. Since a #"C = C"# double bond is stronger than a #"C - C"# single bond, due to the presence of a #pi# bond, it follows that the #"C = C"# bonds must have a shorter bond length than the #"C - C"# bonds. Observe that benzene is composed of both #"C - C"# single bonds, and #"C = C"# double bonds. These appear to be simple mirror images of each other, but this in fact represents a process that occurs continuously throughout the lifetime of a benzene ring.

Shown below are the two resonance structures of benzene: Resonance refers to the existence of numerous forms of a compound, and is a component of valence bond theory.


 0 kommentar(er)
0 kommentar(er)
